How to cut pizza

The title of the post is pizza. But the real story is actually hamburger patties. Knowing how to cut a pizza, or rather knowing the relative size of a slice of pizza will make the story about beef patties interesting. The cutting of the pizza is shown in the following pictures.

Figure 1
This is a whole pizza. Only one slice. The relative size of a slice is 1.

Figure 2
Cut the pizza in two equal slices. The relative size of a slice is one-half or 1/2.

Figure 3
Cut the pizza in three equal slices. The relative size of a slice is one-third or 1/3.

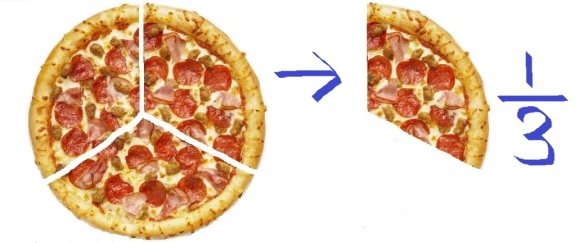
Figure 4
Cut the pizza in four equal slices. The relative size of a slice is one-fourth or one-quarter or 1/4.

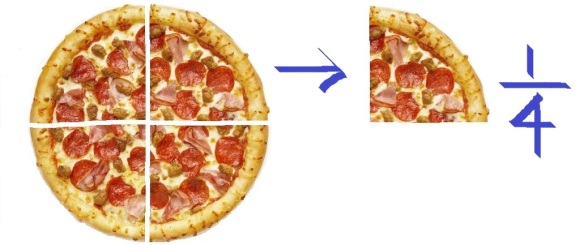
Figure 5
Put the pizza slices together from the smallest to the largest.

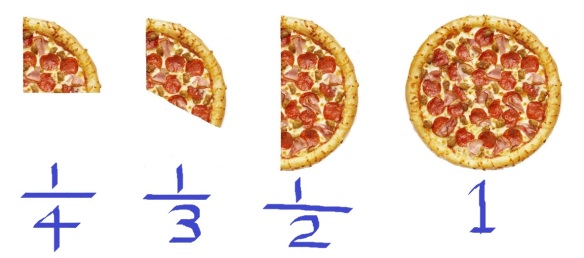
From the last picture, it is clear that one-third of a pizza is bigger than one-fourth or one-quarter of a pizza. The same relativity would apply for other things too. One third of a loaf of bread would be more than one-fourth of the same loaf. Sitting at the doctor’s office waiting for one-third of an hour would be a longer wait than sitting there for one-quarter of an hour. One-third of a gold bar would be more valuable than one-quarter of a gold bar.

At this point, I hope you agree that one-third of any thing is more than one-fourth of that same thing. In particular, one-third of a pound of ground beef would be more meat than one-quarter of a pound of beef. A hamburger patty weights one-third of a pound would contain more beef than a patty that weights one-quarter of a pound.

According to this article in New York Times, many people think the opposite, that one-third pound of beef is less meat than one-quarter pound of beef! The article is a long one about math educational reform efforts in the United States. The following are the two paragraphs relevant to our discussion.

One of the most vivid arithmetic failings displayed by Americans occurred in the early 1980s, when the A&W restaurant chain released a new hamburger to rival the McDonald’s Quarter Pounder. With a third-pound of beef, the A&W burger had more meat than the Quarter Pounder; in taste tests, customers preferred A&W’s burger. And it was less expensive. A lavish A&W television and radio marketing campaign cited these benefits. Yet instead of leaping at the great value, customers snubbed it.

Only when the company held customer focus groups did it become clear why. The Third Pounder presented the American public with a test in fractions. And we failed. Misunderstanding the value of one-third, customers believed they were being overcharged. Why, they asked the researchers, should they pay the same amount for a third of a pound of meat as they did for a quarter-pound of meat at McDonald’s. The “4” in “¼,” larger than the “3” in “⅓,” led them astray.

The participants in the focus groups believed that 1/3 is a smaller number than 1/4 because the 3 in 1/3 is smaller than the 4 in 1/4. How about the public at large? The fact that the new one-third pounder of Whataburger (the parent company of Whataburger is A&W) was a commercial flop while the new burger was favored at taste tests makes it plausible that this was indeed arithmetic failings on the part of the American consumers.

There are two take-aways. One is arithmetic. The fraction 1/3 is bigger than the fraction 1/4. Or put it another way, the fraction 1/4 is smaller than 1/3. This is visually demonstrated in the series of pictures above. The fraction 1/n refers to the situation of dividing one unit of a thing into n equal pieces. More dividing means each fractional piece is smaller. You can view 1/n as the division of one thing among n people. The more people in the division, the smaller each share is for one person. Thus when the number n in the denominator 1/n gets larger, the smaller the share each person would get.

In the pizza example, the more people want to take a share of the same pizza, each person would get a smaller piece. With one million dollars shared by 2 people, each person would get half a million dollars. But with one million dollars shared by one million people, each person can only get one dollar! Again, when the denominator gets larger, the fraction become smaller.

Another way to know the relative size of a fraction is from using a calculator. One divided by 4 gives 0.25, while one divided by 3 gives 0.3333. Note that 0.25 is smaller than 0.3.

The other take-away is that this example is a vivid example of what author John Allen Paulos called innumeracy, which is the mathematical equivalence of not knowing how to read. In fact, he authored Innumeracy: Mathematical Illiteracy and its Consequences. This book is a good read for anyone who wants to improve his or her numeracy or for anyone who wants to understand the issue of innumeracy. It is not a cure for innumeracy, but is a good start.

The New York Times article mentioned above is authored by Elizabeth Green. Here’s another NY Times article that discusses the article by Elizabeth Green.